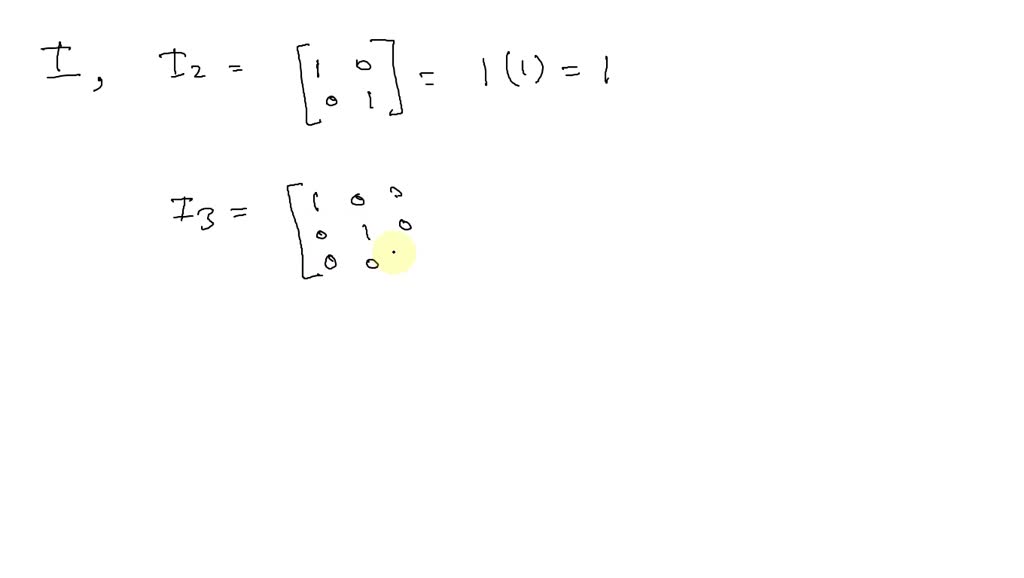Orthogonal Matrix With Determinant 1 . The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof. since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Using the fact that $\det(ab) = \det(a) \det(b)$, we have. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). Det suppose \(u\) is an orthogonal matrix. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. This result follows from the properties of determinants.
from www.numerade.com
Then \(\det \left( u\right) = \pm 1.\) proof. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. This result follows from the properties of determinants. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Det suppose \(u\) is an orthogonal matrix. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. The dot product of any two rows/columns of an orthogonal matrix is always 0. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\).
SOLVEDWhat is the determinant of a unitary matrix? What is the
Orthogonal Matrix With Determinant 1 Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. This result follows from the properties of determinants. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Det suppose \(u\) is an orthogonal matrix. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof.
From www.youtube.com
Orthonormal,Orthogonal matrix (EE MATH มทส.) YouTube Orthogonal Matrix With Determinant 1 a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Det suppose \(u\) is an orthogonal matrix. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; This. Orthogonal Matrix With Determinant 1.
From www.numerade.com
SOLVEDWhat is the determinant of a unitary matrix? What is the Orthogonal Matrix With Determinant 1 Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. The dot product of any two rows/columns of an orthogonal matrix is always 0. Det suppose \(u\) is. Orthogonal Matrix With Determinant 1.
From www.youtube.com
Orthogonal Matrix example YouTube Orthogonal Matrix With Determinant 1 since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. The dot product of any two rows/columns of an orthogonal matrix is always 0. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). Then \(\det \left( u\right) = \pm 1.\) proof. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise. Orthogonal Matrix With Determinant 1.
From fity.club
Orthogonale Matrix Orthogonal Matrix With Determinant 1 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Det suppose \(u\) is. Orthogonal Matrix With Determinant 1.
From www.youtube.com
[Proof] Determinant(s) of an Orthogonal Matrix YouTube Orthogonal Matrix With Determinant 1 Then \(\det \left( u\right) = \pm 1.\) proof. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. Det suppose \(u\) is an orthogonal matrix. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Using the fact that $\det(ab) =. Orthogonal Matrix With Determinant 1.
From www.teachoo.com
Question 8 Evaluate determinant 1 a bc 1 b ca 1 c ab Examples Orthogonal Matrix With Determinant 1 Then \(\det \left( u\right) = \pm 1.\) proof. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. This result follows from the properties of determinants. since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; The dot product of. Orthogonal Matrix With Determinant 1.
From www.studocu.com
Orthogonal Matrices calculus 3 selfmade worksheet Orthogonal Orthogonal Matrix With Determinant 1 (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof. 12 orthogonal matrices in this lecture, we start formally studying. Orthogonal Matrix With Determinant 1.
From www.slideserve.com
PPT Orthogonal matrices PowerPoint Presentation, free download ID Orthogonal Matrix With Determinant 1 a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof. (1) a. Orthogonal Matrix With Determinant 1.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix With Determinant 1 (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Then \(\det \left( u\right) = \pm 1.\) proof. This result follows from the properties of determinants. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose. Orthogonal Matrix With Determinant 1.
From www.numerade.com
SOLVED(10 points) An n X n matrix A is orthogonal if AAT E Find, with Orthogonal Matrix With Determinant 1 (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. Det suppose \(u\) is an orthogonal matrix. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. The dot product of any two rows/columns of an orthogonal matrix is always. Orthogonal Matrix With Determinant 1.
From www.chegg.com
Solved Absolute value of the determinant of the orthogonal Orthogonal Matrix With Determinant 1 Using the fact that $\det(ab) = \det(a) \det(b)$, we have. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and. Orthogonal Matrix With Determinant 1.
From www.youtube.com
Orthogonal Matrix /Definition &Example/TN/12th Maths/Chapter1 Orthogonal Matrix With Determinant 1 Det suppose \(u\) is an orthogonal matrix. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). Then \(\det \left( u\right) = \pm 1.\) proof. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. The dot product of any two rows/columns of. Orthogonal Matrix With Determinant 1.
From www.toppr.com
An orthogonal matrix is Maths Questions Orthogonal Matrix With Determinant 1 The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. Using the fact that $\det(ab) = \det(a) \det(b)$, we have. a n×n matrix a is an. Orthogonal Matrix With Determinant 1.
From www.researchgate.net
Quantum Determinant Sampling circuit for an orthogonal matrix A = (a 1 Orthogonal Matrix With Determinant 1 This result follows from the properties of determinants. 12 orthogonal matrices in this lecture, we start formally studying the symmetry of shapes, combining group theory with linear algebra. Det suppose \(u\) is an orthogonal matrix. The dot product of any two rows/columns of an orthogonal matrix is always 0. (1) a matrix is orthogonal exactly when its column. Orthogonal Matrix With Determinant 1.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Orthogonal Matrix With Determinant 1 a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. The dot product of any two rows/columns of an orthogonal matrix is always 0. Then \(\det \left( u\right) = \pm 1.\) proof. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). since $q$ is. Orthogonal Matrix With Determinant 1.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Orthogonal Matrix With Determinant 1 Det suppose \(u\) is an orthogonal matrix. Then \(\det \left( u\right) = \pm 1.\) proof. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. This result follows from the properties. Orthogonal Matrix With Determinant 1.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix With Determinant 1 Using the fact that $\det(ab) = \det(a) \det(b)$, we have. Then \(\det \left( u\right) = \pm 1.\) proof. Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. The dot product of any two rows/columns of. Orthogonal Matrix With Determinant 1.
From www.scribd.com
Orthogonal Properties PDF Matrix (Mathematics) Determinant Orthogonal Matrix With Determinant 1 Recall that for any matrix \(a\), \(\det(a)^t = \det(a)\). Then \(\det \left( u\right) = \pm 1.\) proof. since $q$ is orthogonal, $qq^t = i = q^tq$ by definition. This result follows from the properties of determinants. Det suppose \(u\) is an orthogonal matrix. The dot product of any two rows/columns of an orthogonal matrix is always 0. a. Orthogonal Matrix With Determinant 1.